LOGIC

Representation in Logic

·         Perhaps the oldest form of knowledge representation is logic, the scientific study of the process of reasoning and the system of rules and procedures that aid in the reasoning process.

·         Logic is considered to be a subdivision of philosophy.

·         The development and refinement of its processes are generally credited to the ancient Greeks.

·         The general form of any logical process is illustrated in the following figure:

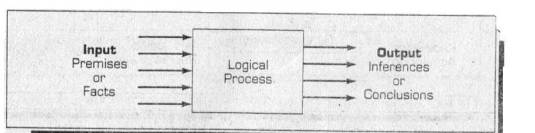
Using Logic to Reason

·         First, information is given, statements are made, or observations are noted.

·         These form the inputs to the logical process and are called premises.

·         The premises are used by the logical process to create the output which consists of conclusions called inferences.

·         With this process, facts that are known to be true can be used to derive new facts that also must be true.

·         For a computer to perform reasoning using logic, some method must be used to convert statements and the reasoning process into a form suitable for manipulation by a computer.

·         The result is what is known as symbolic, or mathematical, logic.

·         It is a system of rules and procedures that permit the drawing of inferences from various premises using a variety of logical techniques.

·         The two basic forms of computational logic are propositional logic (or propositional calculus) and predicate logic (or predicate calculus).

·         The term calculus here does not refer to the differential and integral calculus which we ordinarily associate with the term.

·         Instead, calculus simply refers to a system for computing.

 Propositional Logic

o        A proposition is nothing more than a statement that is either true or false.

o        Once we know what it is, it becomes a premise that can be used to derive new propositions or inferences.

o        Rules are used to determine the truth (T) or falsity (F) of the new proposition.

o        In propositional logic we use symbols such as letters of the alphabet to represent various propositions, premises, or conclusions.

o        For example, consider the propositions used as follows in this simple deductive process:

Statement: A = The mail carrier comes Monday through Saturday.

Statement: B = Today is Sunday.

Conclusion: C = The mail carrier will not come today.

o        Single, simple propositions like these are not very interesting or useful.

o        Real-world problems involve many interrelated propositions.

o        To form more complex premises, two or more propositions can be combined using logical connectives.

o        These connectives or operators are designated as AND, OR, NOT, IMPLIES, and EQUIVALENT.

o        The meanings of each of these connectives and the symbols used to represent them are given in the following figure:

Logical Connectives, or Operators, and Their Symbols

o        These symbols are the same as those used in Boolean algebra.

o        In fact, because propositional logic involves only the truth or falsity of propositions, Boolean algebra and all of the related techniques used in analyzing, designing, or simplifying binary logic circuits can be used in propositional logic.

o        Connectives are used to join or modify propositions to make new propositions.

o        Some examples will show what we mean.

 NOT

o        A truth table can be used to show all possible combinations of this connective.

A = It is raining today.

NOT A = It is not raining today.

o        This truth table shows that if proposition A is true, then NOT A is false.

o        If proposition A is false, then NOT A is true.

 AND

o        When the AND connective is used to combine two propositions, the resulting new proposition is true if both of the original propositions are true.

D = The car is black.

E = The car has a six-cylinder engine.

F = The car is black AND has a six-cylinder engine.

F = D AND E

o        In this case, F is true only if D AND E are true.

 OR

o        When the OR connective is used to combine propositions, the new proposition is true if either one or both of the original propositions are true.

P = The moon is a satellite.

Q = The earth is a satellite.

R = P OR Q – The moon OR the earth is a satellite.

o        A truth table can be used to illustrate all possible combinations of the OR connective.

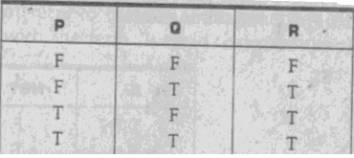
o        You can see that the new proposition R is true if P is true, Q is true, or both P and Q are true.

o        This form of OR is known as the inclusive OR.

o        Another form of the OR connective is the exclusive OR which means that either one proposition (P OR Q) or the other is true, but not both.

 IMPLIES

o        The IMPLIES connective means that if proposition A is true, then proposition B is also true.

o        The truth of A implies the truth of B:

A -----> B

Example: A = The car’s engine is defective.

     B = I cannot drive today.

     C = A IMPLIES B

o        Another way to explain IMPLIES is to use an IF-THEN arrangement.

o        In this example, we can say that IF the car’s engine is defective, THEN I will not drive today.

o        This truth table illustrates the IMPLIES functions.

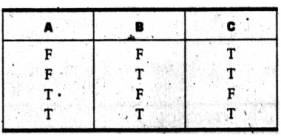
o        The IMPLIES function is somewhat difficult to understand.

o        The way to look at this is that the new proposition C is true if A is false OR B is true.

o        Written logically, this is NOT A, OR B.

o        You can see that B is true in the second and fourth entries in the truth table.

o        A is false in the first and second entries.

o        As a result, the first, second, and fourth entries are true.

o        The only time C is false is when A is true and B is false: A AND NOT B.

o        By using symbols for the various propositions and relating them with connectives, a complete set of premises with resulting conclusions can be expressed.

o        The resulting symbolic expression looks very much like a math formula.

o        It can then be manipulated using the rules of propositional logic or Boolean algebra to infer new conclusions.

o        The truth or falsity of a conclusion can be determined from a wide variety of premises.

 Predicate Calculus

o        Although propositional logic is a knowledge representation alternative, it is not very useful in AI.

o        Since propositional logic deals primarily with complete statements and whether they are true or false, its ability to represent real-world knowledge is limited.

o        (It cannot make assertions about the individual elements that make up the statements.)

o        Consequently, AI uses predicate logic instead.

o        Predicate logic is a more sophisticated form of logic that uses all the same concepts and rules of propositional logic.

o        It gives added ability to represent knowledge in finer detail.

o        Predicate logic permits you to break a statement down into component parts, namely an object, a characteristic of the object, or some assertion about the object.

o        Predicate calculus allows you to separate a statement or proposition into the objects about which something is being asserted and the assertion itself.

o        In addition, predicate calculus lets you use variables and functions of variables in a symbolic logic statement.

o        The result is a more powerful knowledge representation scheme that is far more applicable to practical problem solving on a computer.

o        Predicate calculus is the basis for the AI language called PROLOG (programming in logic).

o        In predicate calculus, a proposition is divided into two parts, the arguments (or objects) and the predicate (or assertion).

o        The arguments are the individuals or objects about which an assertion is made.

o        The predicate is the assertion made about them.

o        In a common English language sentence, objects and individuals are nouns that serve as subjects and objects of the sentence.

o        Once knowledge is organized as either propositional or predicate logic, it is ready for inferencing.