PROBLEM
REPRESENTATION AND PROBLEM-SOLVING STRATEGIES
·
To understand how AI and particularly expert systems
operate, it is necessary to know the process of problem solving and the
approaches used by AI.
Problem Solving and Decision Making
·
Problem solving is often associated with the
performance output of thinking creatures.
·
It is a mental activity of finding a solution to a
problem.
·
The term problem, however, is somewhat misleading.
·
We usually infer that a problem means dealing with
trouble or distress.
·
Although this is true in some cases, it is not true
in all situations.
·
For example, analyzing a potential merger, which is
an examination of opportunity, can be considered problem solving, and so is the
discovery of a new technology.
·
The term problem solving was introduced by
mathematicians.
·
In the world of business, the term decision making
is routinely used as equivalent to problem solving.
·
The AI community uses problem solving fairly
commonly.
The Process of Problem Solving
·
The process of problem solving is viewed differently
by researchers depending on their education and experience.
·
For example, Bell et al. describe several approaches
to problem solving and decision making ranging from the purely quantitative to
one that is based solely on intuition.
·
Six major steps are generally observable in the
process: problem identification and definition, identification of criteria for
finding a solution, generation of alternatives, search for solution and
evaluation, choice and recommendation, and implementation as shown in the
following figure:
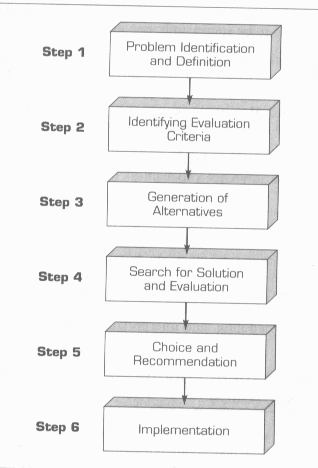
Problem-Solving Process
·
Some scholars use different classifications.
·
For example, Simon’s classical approach identifies
three phases: intelligence, design, and choice.
·
A brief definition of each of the steps follows:
Step 1-Problem
Identification and Definition
o
A problem (or opportunity) must first be recognized.
o
Its magnitude and importance are determined and
defined.
Step
2-Identification of Criteria
o
Solution to a problem depends on the criteria used to
judge the possible alternatives.
o
For example, finding a good investment depends on
criteria (or objectives) such as safety, liquidity and rate of return.
o
In this step we determine what the criteria are and
their relative importance.
Step 3-Generation of
Alternatives
o
By definition, it is necessary to examine two or
more courses of action (one of which can be doing nothing) to be in a decision
situation.
o
Generation of potential solutions requires
creativity and ingenuity.
Step 4-Search for
Solution and Evaluation
o
This step involves examination of the solution
candidates in light of the criteria outlined earlier.
o
It is basically a search process since we are
looking for the best or "good enough" solutions.
o
Several search, evaluation, and reasoning
methodologies can be used in this step.
Step 5-Choice and
Recommendation
o
The product of a search is selecting a solution to
recommend as a remedy for the problem.
Step
6-Implementation
o
To solve the problem, the recommended solution needs
to be successfully implemented.
Human Problem Solving-An Information
Processing Approach
·
This approach is based on the belief that problem
solving can be understood as information processing; it is based on a cognitive
approach that uses a qualitative description of the ways in which people are
similar and of the manner in which people think.
Problem Solving in AI
·
Applied AI technologies are being associated
primarily with the search and evaluation steps of the problem-solving process.
·
The objective is to automate these steps as much as
possible.
·
First let us look at search strategies in general,
and then identify those that are used in AI.
Search Approaches
o
Many approaches and strategies are used to search
for an appropriate solution to problems.
o
Some of these approaches are informal; they involve
intuition, "gut feeling," or just acting on impulses.
o
Formal approaches can be classified into three
categories: optimization, blind search, and use of heuristics.
o
Optimization involves numeric, quantitative
analysis, whereas blind search and heuristics may involve either numeric or
qualitative (symbolic) analysis.
Optimization
o
Optimization attempts to find the best possible
solution by using mathematical formulas that model specific situations.
o
The problem domain must be fairly structured, and
the optimization is conducted by using either a one-step formula or an
algorithm.
o
Recall that an algorithm is a step-by-step search
process in which solutions are generated and tested for possible improvements.
o
An improvement is made whenever possible and the new
solution is subjected to an improvement test.
o
The process continues until no further improvement
is possible.
o
Optimization is used extensively in non-AI
technologies such as operations research (management science) and mathematics.
o
In AI, blind search and heuristic search are used
extensively.
Blind Search
o
In conducting a search, a description of a desired
solution is given.
o
This is called a goal.
o
For example, a goal can be to identify the best
location for a plant or to approve or disapprove a request for a loan.
o
Blind search techniques explore the alternatives and
events of a decision situation, one at a time.
o
Two types of blind search exist.
o
In complete (exhaustive) enumeration all
alternatives are considered; therefore, an optimal solution is discovered.
o
In incomplete (partial) search, the search continues
until a good enough solution is found.
o
In blind situations the search path is arbitrary.
o
No intelligent decision making is employed to direct
the search.
o
There are practical limits on the amount of time and
computer storage available for blind searches.
Heuristic Search
o
For many applications, it is possible to find
specific information to guide the search process and thus reduce the amount of
computation.
o
This is called heuristic information, and the search
procedures that use it are called heuristic search methods.
o
Webster's New World Dictionary defines heuristic as
"helping to discover or learn."
o
There are other definitions.
o
As an adjective, heuristic means serving to
discover.
o
As a noun, a heuristic is an aid to discovery.
o
A heuristic contributes to the reduction of search
in a problem-solving activity.
o
Heuristics (derived from the Greek word for
discovery) are decision rules regarding how a problem should be solved.
o
Heuristics are developed on a basis of solid,
rigorous analysis of the problem and sometimes involve designed
experimentation.
o
Problem solving based on heuristics is a very old
practice in comparison to science based on reason.
o
Several terms are used in practice to describe the
use of heuristics: hints, intuition, judgment, rules of thumb, and inspiration.
o
Heuristic search is much faster and cheaper than a
blind search.
o
The results are considered good enough, and in the
case of quantitative analysis they are very close to optimal solutions.
Search Directions
o
A search in AI can be goal directed, data directed,
or a combination of both.
Data-Directed
(Forward) Search
o
A data-directed search starts from available
information (or facts) and tries to draw conclusions regarding the situation or
the goal attainment.
o
For example, if a company is losing sales volume,
the search attempts to find out why (e.g., because of insufficient
advertising).
Goal-Directed
(Backward) Search
o
A goal-directed search starts from expectations of
what the goal is or what is to happen; then it seeks evidence that supports (or
contradicts) those expectations (or hypotheses).
o
For example, we expect that sales declined because
we think our advertising budget is insufficient.
Problem Representation in AI
·
To understand how the blind and the heuristic
searches work, it is necessary first to illustrate how problems are represented
in AI.
State-Space
Representation
o
The general process of solving any problem using AI
involves three major elements: problem states, a goal, and operators.
o
Problem states define the problem situation and
existing conditions.
o
States are snapshots of varying conditions in the
environment.
o
For example a state can be "you cannot start
your car," or "there is an oil leak."
o
States can also be potential alternative solutions
to problems.
o
All states are unique.
o
The goal is the objective to be achieved, a final
answer, or a solution; for example your goal is finding what is wrong with your
car.
o
There may be more than one goal.
o
Operators are procedures used for changing from one
state to another.
o
An operator describes a process whereby some action
is taken to change initial state into another state that more closely
approaches the goal.
o
Operators move the problem from one state to the
next, following the guidance of a master control strategy, until a goal is
reached.
o
An operator could be an algorithmic subroutine.
o
Following figure shows the relationship between the
initial state, procedures, and goal:
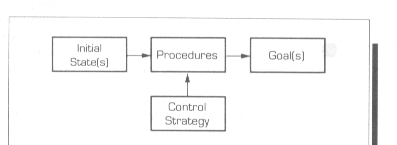
Relationship between Initial
State(s), Procedures, and Goal(s) in the Search Process
o
The initial conditions provide the states that are
manipulated by procedures to achieve the goal.
o
A control strategy selects or guides the procedures.
Graphic
Presentations
Directed State Graph
o
Following figure is a state graph for a simple
problem: attempting to find the best path from one city, the source (S), to
another city, the destination, or goal (G).
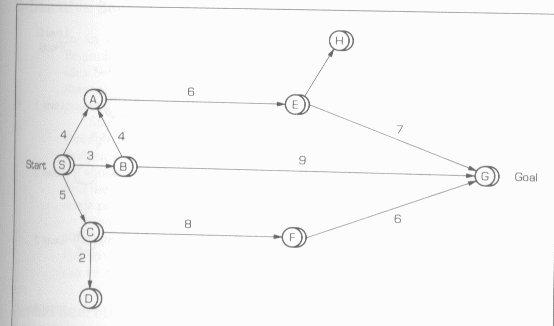
State Graph Showing Alternate
Routes from the Start (S) to the Goal (G)
o
This state graph is a map showing the various
intermediate towns and cities that would be passed through in reaching the
desired destination.
o
In such a problem, there often will be several
alternative routes.
o
The problem is to reach the destination in the least
amount of time, or using the shortest route.
o
The nodes in a state graph are interconnected by
arcs, or links, which usually have arrows showing the direction from one state
to the next.
o
The arcs represent the application of an operator to
a node.
o
The numbers on the arcs represent the distance (or
travel time) between nodes.
o
In practice, it is difficult to represent a state
graph such as that in the above figure in a software form.
o
For example, some of the paths through the state
graph can be retraced repeatedly.
o
The path "S to node B to node A back to node
S" could be repeated over and over again.
o
Such endless loops cannot be tolerated in a computer
program and, therefore, some procedure must be followed to eliminate undesired
cyclical conditions such as this.
o
This is done by converting the state graph into a
search tree.
Search Tree
o
A search tree based on the state graph in the above figure
is illustrated in the following figure:
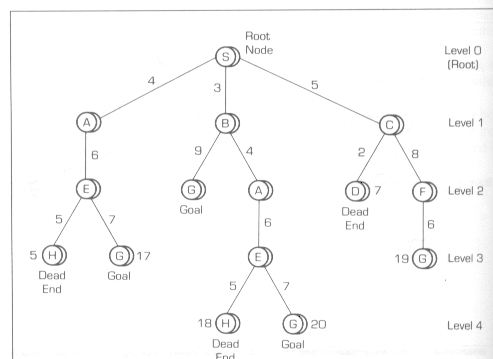
Search Tree
o
The new tree diagram states the same problem but in
a slightly different format.
o
The network thus formed is more like a hierarchy.
o
Note that some of the nodes are repeated to
eliminate the cyclical loop problem described earlier.
o
A special language has been developed to describe a
search tree.
o
For example, the initial state node is called the
root node.
o
It usually describes the object (or topic).
o
Other nodes branch out from the root.
o
These successor, or descendant, nodes are also
sometimes referred to as children.
o
They are intermediate nodes.
o
Working backwards through the tree, nodes are said
to have predecessors, ancestors, or parents.
o
Nodes with no children or successors are called leaf
nodes.
o
They designate the end of the search, either by
arriving a goal or by being at a dead end.
o
The interconnecting arcs are referred to as
branches.
o
Note in the above figure that a search tree is
divided into various levels that are a function of the hierarchy.
o
These levels describe the depth of the tree.
o
The root node is usually designated level 0, and
successively deeper levels are designated sequentially from numbers 1 through
the highest level required to represent the state space.
o
AND/OR branches are another aspect of search trees.
o
The branches from a node to its successors can
represent two or more alternative paths to subgoals.
o
One path or another could lead to the goal.
o
We call these OR nodes because one branch, OR
another, OR another could be the path to the goal.
o
In some problems, however, the successor nodes might
represent problem states that must all be achieved or traversed before the goal
is reached.
o
These are referred to as AND nodes.
o
One subgoal AND another subgoal (AND possibly
others) must be achieved to solve the problem.
o
A search tree is also known as problem reduction
representation because it can be used to divide a problem into subproblems in a
clear way.
Blind Search Methods
·
A blind search is a collection of procedures used
arbitrarily to search a state space.
·
Blind search methods can be classified as exhaustive
or partial (as shown in the following figure), and the two partial methods are
distinguished as breadth-first and depth-first methods:
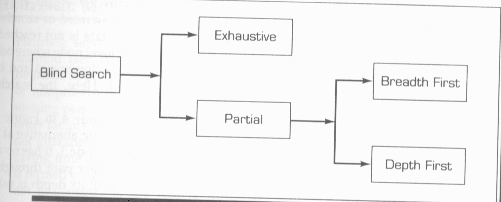
Blind Search Methods
Exhaustive Search
o
In an exhaustive search operators are used to
generate successor states.
o
Beginning at the root node, the search continues
until a solution is found.
o
The idea behind an exhaustive search is to examine
the entire tree in an orderly manner, using all the operators and generating as
many successor nodes as possible to find the desired solution.
o
Starting with the root node, several procedures are
possible for proceeding through the tree; but the approaches are usually
inefficient.
o
In very large problems, a huge number of new states
are generated and many alternatives are considered.
o
As a result, it takes a considerable amount of time
and effort to find the solution.
o
Very-high-speed computers make blind search
acceptable for some problems; however, others are too large for an exhaustive
search.
o
Consider the possible number of moves in a chess
game-estimated to be 10 to the 120th power.
o
For such cases, a heuristic search is more
appropriate.
o
However, for many other cases the following two
partial blind search methods can be effective.
Partial Search
Breadth-First Search
o
A breadth-first search examines all of the nodes (states)
in a search tree, beginning with the root node.
o
The nodes in each level are examined completely
before moving on to the next level.
o
A simple breadth-first search is illustrated in the
following figure:
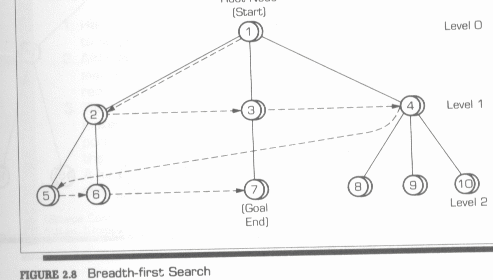
Breadth-First Search
o
The numbers inside the node circles designate the
sequence in which the nodes are examined.
o
In this instance, the search (follow the broken
line) would actually end at node 7, as that is the goal state.
o
A breadth-first search of the state space will
usually find the shortest path between the initial state and the goal state,
with the least number of steps.
o
The process usually starts at the initial state node
and works downward in the tree from left to right.
o
A terminal node is not necessarily a goal node; it
can be a dead-end node.
o
Breadth-first procedures are good when the number of
paths emanating from each goal is relatively small and where the number of
levels in each branch is of a different depth (number of levels).
Depth-First Search
o
A depth-first search begins at the root node and
works downward to successively deeper levels.
o
An operator is applied to the node to generate the
next deeper node in sequence.
o
This process continues until a solution is found or
backtracking is forced by reaching a dead end.
o
A simple depth-first is illustrated in the following
figure:
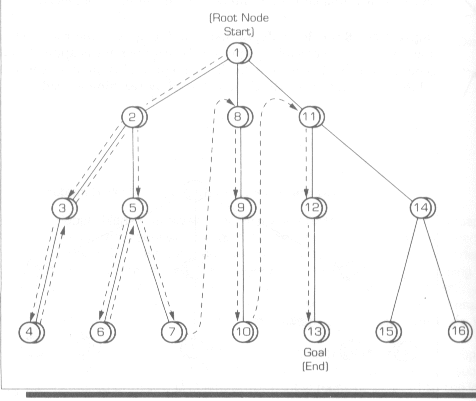
Depth-First Search
o
Again, the number inside the nodes designate the
sequence of nodes generated or searched.
o
This process seeks the deepest possible nodes.
o
If a goal state is not reached in this way, the
search process backtracks to the next highest level node where additional paths
are available to follow.
o
This process continues downward and in a
left-to-right direction until the state goal is discovered.
o
Here, the search would actually end at node 13.
o
When a dead-end node is discovered, such as node 4
in the above figure, the search process backtracks so that any additional
branching alternative at the next higher node level is attempted.
o
The search backs up to node 3.
o
It has no alternate paths, so the search backtracks
to node 2.
o
Here, another path through node 5 is available.
o
The path through node 6 is explored until its depth
is exhausted.
o
The backtracking continues until the goal is
reached.
o
The depth-first search guarantees a solution, but
the search may be a long one.
o
Many different branches will have to be considered
to a maximum depth before a solution is reached.
o
(By setting a "depth bound," it is
frequently possible to reduce the search.)
o
The method is especially attractive in cases where short
paths exist and where there are no lengthy sub-branches.
Heuristic Method
·
Heuristic search methods are designed to reduce the
amount of search for a solution.
·
When a problem is presented as a search tree, the
heuristic approach attempts to reduce the size of the tree by pruning nonvital
or nonpromising nodes.
·
For example, when the Coast Guard searches for a
missing person at sea, they don’t check the entire ocean.
·
Currents, winds, and other factors are used to limit
the search area.
·
Although such an approach does not guarantee that
the person will be found, it does work well in most cases, saving time and
expediting the search.
·
Such an approach is not optimal, so it is termed
good enough.
·
The question is to determine what to consider and
what not to consider in the search.
·
There are several methods, or approaches, to answer
such a question.
·
Heuristics do, however, have some limitations.
Representative
Approaches
Generate and Test
o
The basic idea is to generate (via rules) possible
candidate solutions and devise a test to determine if the solutions are indeed
good.
o
An example is opening a combination lock without
knowing the combination.
o
One way to execute this search is to follow a
five-step procedure (suggested by Wolfgram et al.):
1.
Add a specification criterion (e.g., a known symptom,
such as it is common to open a combination lock by turning it first to the
left).
2.
Try a path that satisfies the specification.
3.
Determine whether the path is plausible;
"prune" that path if it is not plausible.
4.
Move to the next path.
5.
Check to see if all specifications have been mentioned.
If not, add the next specification criterion
and reiterate the steps by returning to step 1.
If all specifications have been resolved, the
process is complete.
o
The generate and test method is effective only if
pruning can be done early in the search so many paths can be eliminated.
Hill Climbing
o
The hill-climbing method is similar to a depth-first
blind search.
o
However, paths are not selected arbitrarily, but in
relationship to their proximity to the desired goal.
o
The search tree in the following figure illustrates
the concept:
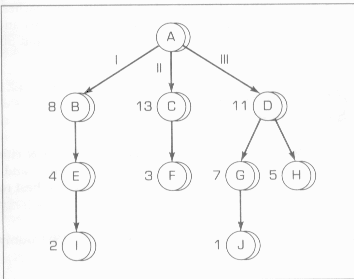
Hill Climbing
o
Each production process I, II, and III can continue
for several stages, in which several states (nodes) exist.
o
The numbers above the nodes designate the potential
number of defects in a specific product at a certain state in the process.
o
The more stages we go through, the fewer defects we
will find.
o
The target is to find the method with the minimum number
of defects.
o
A depth-first search goes to I, then to II, and then
to III.
o
If the desired number of defects is two, then the
process is speedy.
o
But, if the goal is one defect, then the entire tree
will have to be visited.
o
In the hill-climbing method, nodes B, C, and D are
compared, and a search starts in branch I (the lowest number of defects-8).
o
Since one defect was not discovered, backtracking is
done to branch III.
o
(Ill is done before II since there are fewer defects
on D than on C.)
o
The search goes to D and H; backtracking is then
exercised and the D-G-J path leads to the desired solution.
o
Path A-C-F was not visited.
o
Thus, hill climbing is faster than a depth-first
search.
o
Variations of this method exist, and the saving over
a blind search can be substantial if large trees are involved.
Induction
o
Induction means to generalize from a smaller (or
simpler) version of the same problem.
o
Two features of induction are essential.
o
First, in the problem statement the problem must be
modeled in terms of the associated (or predicted) data.
o
Second, the induced result must be tested against
real examples to verify its reasonableness.
Construction
o
The input for methods based on the construction
strategy is the data that defines a specific instance of the problem.
o
A solution is built up one component at a time.
o
A construction strategy begins by examining this data
and attempting to identify an element that is likely to be a valuable part of a
good final solution.
o
Next, successive additional elements of a solution
are added.
o
Once the final solution has been built up, it may be
obvious that improvement can be made.
o
Therefore, the hill-climbing procedure is often
applied to the output of the construction method.
Component Analysis
Strategy
o
Some problems are so large or so complicated that the
only practical approach is to break them into manageable portions.
o
These portions are then dealt with independently by
heuristics and/or algorithms.
o
The solutions for the portions are then combined.
o
Of course, it may be extremely difficult to piece
the solutions to the different components into an acceptable plan.
o
This approach is also called the decomposition
method.
Best First
o
In the best-first approach, which is based on some heuristic
evaluation function, you select the next move by searching for the best
available solution that you can move to in one step, no matter where it is
located on the tree.
o
For example, you are about to cross a stream and
there are many rocks on your way.
o
First you go the most promising one, then you look
around and make the best progress you can.
o
If you evaluate only one jump at a time, you are
using the best-first approach.
o
This procedure is often labeled "greedy,"
since it is shortsighted.
o
It searches only one step at a time instead of
looking at the entire set of steps.
o
An implementation of the best-first approach is
called the A* algorithm.
Other Approaches
o
Several other heuristic approaches can be useful,
especially when numeric analysis is involved.
Control Strategies
·
Once a search method is selected it needs to be
activated.
·
That is, it is necessary to decide which operators
to apply and when to apply them.
·
In a rule-based system, for example, we must decide
which rule to check next.
·
Four basic control strategies are common: forward
chaining, backward chaining, means-end, and least commitment.
Forward Chaining
o
The forward chaining method emulates human deductive
reasoning.
o
It is a data-driven process that starts when certain
information is provided by the user.
o
Clues are collected as we move toward a conclusion.
Backward Chaining
o
Backward chaining is a goal-driven search strategy.
o
It begins with the goal and works backward towards
the initial conditions.
o
The process starts with a hypothesis; a search is
then launched to find and verify the necessary supporting facts.
o
The process ends with the acceptance or rejection of
the hypothesis.
Means-End Analysis
o
Means-end analysis is an iterative process of
subdividing the difference between the current state and the goal state until
the difference is eliminated.
o
The solution shows the means by which to traverse
the knowledge base.
o
The method applies a set of operators that assist in
moving us toward the goal.
o
The method attempts to achieve the difference
reduction in the most efficient manner; that is, by selecting the appropriate
operators, in the proper sequence.
o
For example, you live in a ranch near Austin, Tex.,
and you would like to see the Statue of Liberty in New York.
o
You have a short vacation.
o
The distance between Austin and New York is about
1,800 miles (the "difference").
o
The operator that is most effective in reducing this
difference is to "fly."
o
To activate this operator you need to reach an
airport which is 23 miles away.
o
Now you need a means to satisfy a subgoal of getting
to the airport.
o
For that you need another operator (e.g., drive or
be driven in a cab).
o
In either case, you have to get a car; similarly,
several more operators will be needed to help reach your goal.
Least Commitment
o
According to the least commitment control strategy,
we assume that no decision should be made until there is enough information.
o
To activate this approach, we need to know what is
"enough information."
o
Also, we need to know what to do when there is not
enough information (e.g., how to get additional information, or when to make a
guess).
o
This control strategy could be combined with neural
computing to increase the reliability of the "guesses."
·
Control strategies are implemented by a control
program called the inference engine.
·
The program determines how and in what sequence the
state space, which is the knowledge base, is searched.
·
The inference engine and the knowledge base are the
two major components of the most widely used AI technology-expert systems.
